Por Gabriel Escalante Fat

                Cuando el ex Beatle Paul Mc Cartney escribió en 1967 la canción “When I am sixty four”, tenía 25 años y consideraba que los 64 eran una edad para estar retirado, haciendo sencillas labores domésticas y entreteniendo a sus nietos sobre las rodillas. Seguramente nunca imaginó que a los 82 él seguiría siendo un “monstruo escénico” capaz de dar un show de tres horas ante un estadio lleno.

                Pues bien, hace pocos días alcancé esa mítica y mágica edad: 64. No tengo nietos aún, ciertamente he perdido parte de mi cabello sin que todavía se me pueda considerar calvo, y hago bastante más que sencillas labores domésticas, tanto por gusto como por necesidad.

              No hubo fiesta, pero no quise que la fecha pasara inadvertida. Mi primera actividad de la mañana, muy temprano, fue sumergirme desnudo en un cenote de la península de Yucatán, dentro de una bellísima caverna.  Allí, en total contacto con un agua de transparencia impresionante, en casi completo silencio (el parque abriría al público una hora más tarde) emulé un regreso simbólico al vientre materno del que salí 64 años antes.  ¡Una grata experiencia!

——————————————–

                El 64 es un número muy elegante, de acuerdo a los matemáticos. Es divisible entre 2, 4, 8, 16 y 32.  Sus raíces cuadrada, cúbica, cuarta y sexta son números enteros y es el número de casillas que tiene un tablero de ajedrez, en opinión de muchos el más apasionante juego de mesa jamás inventado, al grado de que ha sido calificado como el “deporte ciencia”.  

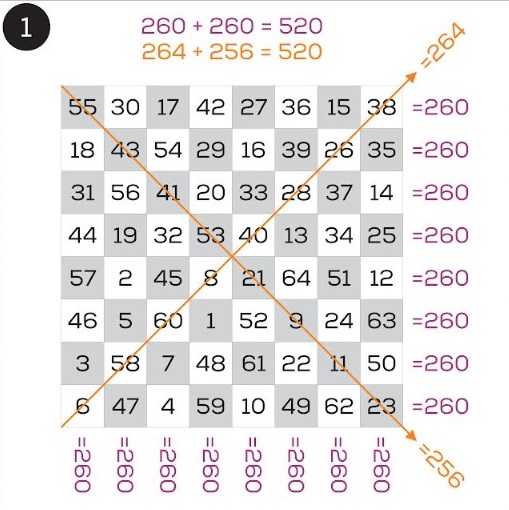
                Utilizando el tablero de ajedrez, un cuadrado dividido en 64 cuadros, 8 por lado, se han creado, como divertimento matemático los llamados “cuadrados mágicos”, con características curiosas como que las sumas de cada una de sus filas, horizontales y verticales sea la misma cantidad, en este caso 260, que es la octava parte de la suma de los números consecutivos del 1 al 64 = 2,080.  Ilustro esto con el cuadrado creado por el ajedrecista ruso-finlandés del siglo XIX, Carl Ferdinand Jaenisch.  ¨

                Este cuadrado tiene, además, la particularidad de que sus diagonales extremas suman 256 y 264, respectivamente, que en conjunto nos dan 520, el doble de los 260 que suma cada línea recta.  (Imagen 1).

                Además, al igual que la diagonal principal ascendente (que suma 264) las diagonales paralelas fragmentadas en el mismo sentido, también suman 264 (para mayor facilidad, las he coloreado en tonos iguales cada una). (Imagen 2)

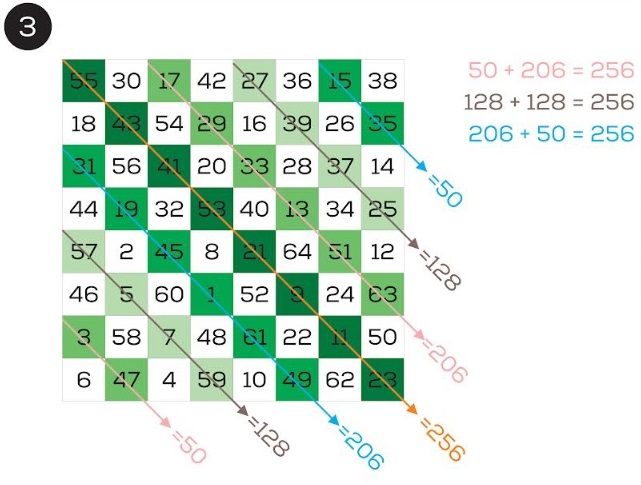
                Lo mismo sucede con la diagonal principal descendente (que suma 256), con sus diagonales paralelas fragmentadas. (Imagen 3)

                Por si esto fuera poco, este cuadrado mágico se puede recorrer en orden, desde el 1 hasta el 64, con los movimientos del caballo del ajedrez, en un recorrido que tiene una impresionante simetría. (Imagen 4)

                Para concluir, dejo aquí el relato que leí por primera vez hace más de 50 años, en un viejo libro del autor ruso Yakov Perelman, titulado “Matemáticas recreativas”, en cuyo capítulo “Historias sobre números gigantes”, narra esta leyenda hindú que relaciona las matemáticas con el ajedrez.  La escribí más o menos de memoria y buscando datos en la Internet, acerca de las cifras y de cómo concebirlas de manera concreta.

LA RECOMPENSA

                Cuenta la leyenda que, cuando el rey hindú Sheram conoció a Seta, el inventor del ajedrez, lo mandó llamar para recompensarlo por tan genial creación.

                El sabio Seta, quien vivía de lo que le pagaban sus discípulos, vestía con sencillez y actuaba con humildad y respeto.

                —Seta, quiero recompensarte dignamente por el ingenioso juego que has inventado —dijo el rey. —Soy bastante rico como para cumplir tu deseo más elevado, di la recompensa que te satisfaga y la recibirás.

                Después de un momento de silencio, Seta agradeció la magnanimidad de su soberano y le pidió un día para meditar en la recompensa.

                Cuando al día siguiente se presentó el sabio, su petición dejó maravillado al rey, por su modestia.

                —Soberano, manda que me entreguen un grano de trigo por la primera casilla del tablero de ajedrez.

                —¿Un simple grano de trigo? —contestó admirado el rey.

                —Sí, soberano.  Por la segunda casilla, ordena que me den dos granos; por la tercera, cuatro; por la cuarta, ocho; por la quinta, dieciséis; por la sexta, treintaidós…

                —¡Basta! —le interrumpió, molesto, el rey.  —Recibirás el trigo correspondiente a las 64 casillas, de acuerdo a tu deseo: por cada casilla, doble cantidad que por la anterior.  Pero debes saber que tu petición es indigna de mi generosidad; tu mísera petición menosprecia mi benevolencia. Tendrías que haber dado mayor prueba de respeto ante la bondad de tu soberano. ¡Retírate! Mis servidores te sacarán un saco con la recompensa que solicitas.

                Seta sonrió, abandonó la sala y esperó a las puertas del palacio.

                Unas horas después, el rey se acordó de la recompensa y preguntó si ya habían cumplido con entregarle el trigo a Seta.

                —Soberano, están cumpliendo tu orden. Los matemáticos de la Corte calculan el número de granos que le corresponden.

                El rey se molestó, puesto que no estaba acostumbrado a que tardaran tanto en cumplir una orden dada por él.  Antes de irse a dormir volvió a preguntar si Seta ya se había marchado con su saco de trigo.

                —Soberano, los matemáticos trabajan sin descanso. Esperan tener resuelto el cálculo al amanecer.

                Por la mañana, el matemático mayor de la Corte solicitó audiencia ante el rey.  

En cuanto éste lo recibió, quiso saber si ya habían entregado a Seta su mísera recompensa.

                —De eso precisamente quería hablarle, soberano. Hemos calculado escrupulosamente la cantidad de granos que desea recibir Seta.  ¡Resulta una cifra tan enorme!

                —Sea cual fuere esa cifra, mis graneros no se verán mermados.  He prometido esa recompensa y debo cumplir mi palabra —respondió el rey.

                —Soberano, no depende de su voluntad entregar o no la recompensa. En todos sus graneros no existe la cantidad de trigo que exige Seta. Tampoco existe en todos los graneros del reino. ¡Hasta los graneros del mundo entero serían insuficientes!

                El rey se había quedado sin palabras.

                —Si usted quiere cumplir con su promesa, ordene que todas las tierras disponibles se destinen a cultivar trigo. Mande desecar océanos y siembre en ellos. Derrita los polos y riegue con su agua los campos de labranza.  Sólo entonces podrá el sabio recibir su recompensa.

                —Dime cuál es esa cifra tan monstruosa —ordenó el rey.

                —¡Oh, soberano! Dieciocho trillones, cuatrocientos cuarenta y seis mil setecientos cuarenta y cuatro billones, setenta y tres mil setecientos nueve millones, quinientos cincuenta y un mil seiscientos quince.

                El rey, agobiado, perdió el conocimiento.

                Hasta aquí, la leyenda.

                La cifra, que en números se expresa así: 18 446 744 073 709 551 615 equivale, considerando 20,000 granos por Kilogramo, es decir, 20 millones por tonelada, a

922 337 203 685 (novecientos veintidós mil millones de toneladas), que es alrededor de mil doscientas veces la producción mundial anual de trigo, unas 772 millones de toneladas.

                ¿Cuánto es 772 millones de toneladas? 

                Bien, un vagón de ferrocarril transporta unas 50 toneladas de grano.

                Por tanto, se requerirían 15 millones 440 mil vagones.  Si cada vagón mide unos 19.6 metros de longitud, el hipotético tren que transportara la producción anual de trigo, mediría 302,745 kilómetros de longitud: 7.5 vueltas a La Tierra, 22 veces la distancia de Alaska a la Patagonia, 152 veces la longitud del tendido de vías del Tren Maya.

                En consecuencia, el poderoso soberano Sheram, de haber vivido en la actualidad, debería destinar la producción mundial de trigo por los próximos mil doscientos años, para recompensar adecuadamente al sabio Seta.

Guadalajara, Jalisco, noviembre 13, 2024.

*Contacto: gescalantefat@aol.com

FB: Gabriel Escalante: https://web.facebook.com/gabriel.escalante.31542